Acción Formativa N° 55: “Exploración matemática de la Pirámide en un viaje virtual”

Módulo: Identidades, Cultura y Sociedad

 

Llegamos hoy a ustedes con nuevas ideas, sugerencias y propuestas pedagógicas sobre un tema apasionante: la exploración matemática. Lo hacemos pensando en acompañar a la docencia en sus prácticas de enseñanza.

Seguimos en diálogos con toda nuestra Provincia de Santa Fe, porque nuestro propósito es continuar indagando en los procesos de enseñanza que garanticen el Derecho a la Educación en su sentido más amplio.

Las y los invitamos a compartir esta publicación.

 

Licenciada Nanci Noemí Alario.

Subsecretaria de Educación Primaria.

 

 

1- INTRODUCCIÓN:

El presente material ha sido pensado a fin de aportar ideas para la gestión de la clase de las y los docentes de la provincia en el armado de sus secuencias didácticas, propuestas de actividades y diseño de planificaciones.

La intención es seguir profundizando junto a las chicas y los chicos la construcción de conceptos de medida, equivalencias entre unidades, cálculo y estimación de longitudes y superficies. Si bien esta última, la estimación, puede ser aprendida de forma espontánea en cuestiones diarias no vinculadas a la escolaridad, cobra un papel importante en la enseñanza matemática primaria y debe ser incorporada de manera intencional a fin de que se construya la potencialidad de la misma en diversas situaciones.

El material está pensado dando continuidad a las propuestas de “Alfasueños” para 7mo. grado pero de manera gradual. El abordaje puede comenzar también en años anteriores.

Se entrelazan contenidos de diversas disciplinas posibilitando que la creatividad de las y los docentes pueda ampliar y profundizar el abordaje de los conceptos según el interés de cada grupo de chicas y chicos, el momento del año en que se pone en acto y la relación con los contenidos planificados. 

Se requiere instalar el programa Google Earth o utilizar Google Maps, este último disponible en la mayoría de celulares. Si se carece de estas herramientas proponemos realizar un video con el celular para que las alumnas y alumnos puedan experimentar lo que es un viaje virtual. Pensamos que la creatividad logrará enriquecer la experiencia aún en caso de no contar con los programas sugeridos. 

Con la convicción de que ninguna obra humana es perfecta se podrá potenciar y optimizar el presente trabajo desde la realidad de cada comunidad educativa, del recorrido que se pretende realizar,  tomando como punto de partida los saberes previos de nuestras niñas y niños.

2- RECORDAMOS ACUERDOS IMPORTANTES:

En el marco de los Núcleos de Aprendizajes Prioritarios NAP de 7mo. grado se proponen las siguientes competencias:

EN RELACIÓN CON LA GEOMETRÍA Y LA MEDIDA:

El reconocimiento de figuras y cuerpos geométricos y la producción y el análisis de construcciones explicitando las propiedades involucradas en situaciones problemáticas que requieran:

– Analizar figuras (triángulos, cuadrados) y cuerpos (pirámides) para caracterizarlas.

– Explorar y argumentar acerca del conjunto de condiciones (sobre lados, ángulos, diagonales) que permiten construir una figura (triángulos, cuadrados). 

– Construir figuras a partir de diferentes informaciones (propiedades y medidas) utilizando compás, regla, transportador y escuadra, explicitando los procedimientos empleados y evaluando la adecuación de la figura obtenida.

La comprensión del proceso de medir, considerando diferentes unidades y sistemas, en situaciones problemáticas que requieran:

– Argumentar sobre la equivalencia de distintas expresiones para una misma   cantidad, utilizando las unidades de longitud y área, del SIMELA y sus relaciones.

El análisis y el uso reflexivo de distintos procedimientos para estimar y calcular medidas en situaciones problemáticas que requieran:

– Calcular áreas de figuras y cuerpos, estimando el resultado que se espera obtener y evaluando la pertinencia de la unidad elegida para expresarlo.

– Elaborar y comparar distintos procedimientos para calcular perímetros y áreas de polígonos.
 

3- COMPARTIMOS ALGUNOS SABERES:

El papel de la Matemática en las herramientas tecnológicas es indiscutible, en particular Google Earth y Google Maps incorporan técnicas matemáticas, Geometría el primero y la teoría de grafos el segundo. 

    “Por ejemplo, “en el caso de Google Maps hay una aplicación consistente en calcular el camino más corto entre dos nodos. Cuando uno intenta buscar opciones en Google Maps para ir de un sitio a otro, eso es en esencia un problema de teoría de grafos que en el caso fundamental está resuelto por el algoritmo de Dijkstra”. Este algoritmo, también denominado de caminos mínimos, permite determinar el camino más corto dado un vértice origen al resto de vértices en un grafo con pesos en cada arista.” (“Revista Iberoamericana para la difusión de la ciencia y la tecnología”, 2012)

En las propuestas de trabajo se deja abierta la posibilidad para profundizar en la  geografía matemática que se ocupa de la localización y la representación del espacio de la superficie terrestre, entre otros aspectos. La teoría de grafos no es abordada en esta propuesta pero podría ser un disparador para una nueva. 

La Geometría, como ciencia que estudia el espacio, aporta un marco para la localización, distribución y representación del espacio geográfico. Según Buzai (2006), en las últimas décadas se han desarrollado los Sistemas de Información Geográfica (SIG) que han posibilitado una revolución tecnológica pero por sobre todo una revolución intelectual. La modelización matemática ha ampliado el campo a la disciplina posibilitando una mayor interacción con otras. 

Esta propuesta intenta despertar el interés de conocer la herramienta y por medio de ella desarrollar conceptos geométricos y de medición. Sabemos que “el estudio del espacio no se construye por abstracción directa del espacio real, sino a partir de utilizar las propias conceptualizaciones en la resolución de problemas que plantea dicho espacio.” (Itzcovich, 2012) 

En relación a la Medida, “para que los alumnos puedan aprender los saberes incluidos en los Núcleos de Aprendizajes Prioritarios en la escuela, tendremos que proponer situaciones de enseñanza en la que se pongan en juego distintos aspectos de los mismos.” (MEC, serie Cuadernos para el aula 6, 2006) 

La resolución de situaciones vinculadas a la realidad con el uso de herramientas tecnológicas, despierta una multiplicidad de interrelaciones entre contenidos de diversas disciplinas.

El trabajo con la estimación en medida y la anticipación de resultados es una oportunidad para abrir la discusión al comparar la aproximación realizada con la medición efectiva.    

4-RESOLVEMOS, CREAMOS Y PROPONEMOS:

¿Escuchaste hablar de Google Earth?  Te invitamos a ver este video: 

https://www.youtube.com/watch?v=6ydbEhndVbU

 Para descargar el programa te brindamos el siguiente enlace: 

Descargar programa

Otra herramienta posible es Google Maps. Esta aplicación está incorporada en la mayoría de los celulares.

 

Luego de mirar el video y descargar o entrar en el programa, te proponemos viajar virtualmente. 

Podés visitar los lugares que se te ocurran.

Con cualquiera de estas herramientas podrías recorrer el territorio de tu provincia, tu ciudad, tu pueblo, tu barrio…. Mirar los caminos, las rutas y calles, las vías del tren, ríos, arroyos, diversas construcciones: casas, edificios, plazas, monumentos, fuentes y todo lo que quieras ver de manera casi instantánea.

Comencemos el viaje juntas y juntos: 

1. En el buscador de Google Earth o Google Maps escribí: el nombre del lugar donde vivís.

 

Verás que viajás a una velocidad increíble. 

¿Llegaste?  A medida que te vas acercando  podrás verlo con más detalle.

 

• Observá elementos naturales, campos, ríos,… y otros construidos por el hombre. 
• Buscá tu escuela, tu casa.
• Compará distancias, por ejemplo: ¿Qué tan lejos estás de la escuela?
• Mirá las manzanas que rodean la escuela. 

Si tu escuela está en zona rural o de islas, observá las delimitaciones de los terrenos, ya sean límites naturales y/o artificiales. 

Seguramente has estudiado o escuchado hablar sobre las poblaciones de algunos pueblos de la antigüedad. Uno de ellos es el antiguo Egipto que cuenta con maravillosas y enigmáticas pirámides.

¿Te animás a viajar a Egipto y verlas?

– En el buscador de Google Earth o Google Maps escribe: Egipto.

– Mientras viajás mirá qué oceános, mares, continentes se atraviesan. Observá los colores que se presentan.  

Una vez en Egipto observá y recordá:

+¿Qué representan los azules, los marrones, los verdes…?

+¿Qué es lo que llama más tu atención? 

+¿Por qué será que hay una zona verde entre tantos marrones? 

+¿A qué puede deberse? 

+¿Qué nombre recibe el río que más se destaca? 

+¿Sabías que es uno de los ríos más largos del mundo? 

+ Averiguá cuánto mide y compará su longitud con la de nuestro Río Paraná.

Si te interesa podés profundizar sobre el antiguo Egipto y el crecimiento en las márgenes del río. Pero ahora te invitamos a ver las famosas pirámides de Giza en Egipto. 

En el buscador de Google Earth escribí: Egipto, pirámide de Keops.

Se puede ver la Pirámide desde una vista superior. 

– Representá esta vista en una hoja. 

– ¿Cómo se verá desde otras perspectivas?

– ¿Te animás a dibujarla según la posición del observador: de arriba, de costado, de frente? 

– Podés ir rotando la imagen con el mouse para observar. Estas distintas miradas se denominan “Vistas” y se logran a través de proyecciones gráficas del objeto obteniendo una figura sobre la hoja. Aquí sólo vamos a necesitar un esquema. Pero podés profundizar sobre el tema con tus docentes de Plástica, Tecnología y Matemática trabajando con escalas, proyecciones ortogonales, cortes topográficos, perspectivas isométricas, puntos de fuga.

– Comparte tus dibujos con los de tus compañeras y compañeros. 

– ¿Hubo coincidencias?

La siguiente imagen muestra el esquema de una de las vistas de la pirámide: ¿desde dónde podría haber sido observada? 

– Si tuvieras que dictar a otra persona los pasos que debe realizar para obtener, en una hoja lisa, un dibujo como el de la vista sin mirarlo ¿qué diría ese mensaje? Escribilo.

– Al finalizar se deben superponer los dibujos para verificar que coincidan. 

a- ¿Coinciden? 

b- ¿Tendremos que ajustar la redacción? Podés hacerlo en conjunto. Pensá qué ángulos hay que indicar y qué longitudes. 

c- ¿Cómo podrías ayudarte para indicar matemáticamente las aristas de la pirámide y así ayudar al lector en la construcción?

Volvemos a Egipto:

• ¿Qué nombre matemático recibe la pirámide de Keops según el polígono de la base?
• ¿Qué otros tipos de pirámides hay?
• ¿Qué dimensiones tendrá la pirámide de Keops? Observá y compará con otros elementos del mapa. 

Estimá la medida aproximada de la longitud de cada lado del cuadrado de la base. ¿Qué elementos se ven alrededor que te puedan servir para comparar?

 Observá los vehículos que se encuentran en la cercanía. ¿Cuánto mide un auto aproximadamente? ¿Y un colectivo de viaje? 

¿Se te ocurre otra forma de compararlo?

Mové la ruedita del mouse para acercar y alejar la imagen. 

¿Qué altura aproximada tendrá la pirámide? ¿Será más o menos de 200 m?

¿La superficie de terreno que ocupa será mayor, menor o igual que una manzana de las ciudades y pueblos de nuestra provincia? ¿y que una cancha de fútbol? 

¿Cuántas piletas olímpicas de natación te parece que se podrían construir en una superficie similar a la que ocupa la pirámide (averiguá las dimensiones de una pileta olímpica)?

Para conocer más acerca de las pirámides de Egipto te invitamos a mirar un video en el siguiente enlace:  Pirámide de Keops

Como verás, en el video se respondieron algunas de las preguntas anteriores respecto de las estimaciones que realizaste. Pero ahora manos a la obra, llegó el momento de medir y comprobar.

 

Te propongo efectuar la medición de la longitud del lado de la base de la pirámide con el programa que estamos utilizando. 

 

Teniendo la medida del lado podemos calcular el perímetro y la superficie de la base de la pirámide.

¿Te animás? ¿Cómo escribirías con símbolos matemáticos las fórmulas del perímetro y de la superficie del cuadrado?

Registrá las medidas del lado de la base de la pirámide con la información que te provee la ventana de las mediciones en el programa.

Lado de la base de la pirámide

en metros: ………….….m 

en centímetros: ……….cm

en kilómetros:…………….km

en pulgadas: ….……” (el símbolo de la unidad pulgadas es ”)

¿Cuál es la más apropiada para la longitud que estás midiendo? ¿Hay relación entre las distintas unidades? Observá que algunos números difieren debido al redondeo.

Completá la siguiente tabla sólo con el dato obtenido (en metros) y calculando las equivalencias que se solicitan.  

Compará con las equivalencias obtenidas en el cuadro de mando que se habilita desde la herramienta. ¿Hubo coincidencias? Si las hubo ¿qué conclusiones se pueden sacar? Si no las hubo ¿a qué se debió? ¿Qué se observa respecto del redondeo de cantidades?

Continuamos. Ya habías calculado el perímetro y la superficie de la base de la pirámide conociendo la longitud del lado del cuadrado. 

Ahora vamos a hacerlo con Google Earth: Con la herramienta “polígono” se puede medir el perímetro  y el área  de un territorio indicado por medio de una poligonal cerrada. (Esta herramienta está disponible haciendo clic en la regla. En el cuadro de mando las pestañas indican línea, ruta, polígono, círculo, ruta de acceso 3D, polígono 3D)

Compará el cálculo del área y del perímetro que hallaste con el que aporta la herramienta. ¿Qué conclusiones se pueden enunciar?

Completá estos datos obtenidos con la acción realizada en el programa. (Cambiando la unidad)

Observá que al no poder escribir todas las cifras el programa realiza un redondeo.

Completá la tabla utilizando las equivalencias conocidas y la proporcionalidad, pero antes….

 

Analizá las relaciones de equivalencia que se establecen:

Ya trabajamos con la superficie de la base del cuerpo. Vamos a hallar ahora, de manera aproximada, la superficie lateral de la pirámide en la actualidad y de la pirámide original. 

Para ello observemos:

¿Qué figuras componen sus caras? ¿Cómo son entre sí en este caso? ¿Por qué podés asegurarlo? En las caras, ¿qué medidas de las figuras es necesario conocer para poder hallar la superficie? ¿Con qué datos contamos?

(Como trabajamos de manera aproximada, descartaremos los cm (centímetros) de diferencia que en tan imponente monumento no hacen de la base un cuadrado perfecto. Pero si se desea podría considerarse para habilitar la discusión que abre también a los errores en todo proceso de medición.)

Realizá un esquema que muestre el desarrollo de la pirámide. Colocá las medidas de las longitudes que tenés. ¿Qué nos falta calcular?

altura de la pirámide original = 146,60 m

altura de la pirámide actual = 138 m 

longitud del lado de la base =  ……..

altura del triángulo de la cara lateral de la pirámide =   …….

Ya hemos medido con la regla de Google Earth la longitud del lado de la base de la pirámide.

¿Se te ocurre cómo podremos obtener la altura del triángulo de la cara lateral? Pensá cómo podrías hacerlo. Debatí con tus compañeras y compañeros junto con tu docente.

En un esquema de la pirámide podemos indicar las longitudes. Aquí te propongo tres esquemas desde diversas ópticas:

¿Qué indica la línea color roja? ¿Qué nombre matemático recibe?  

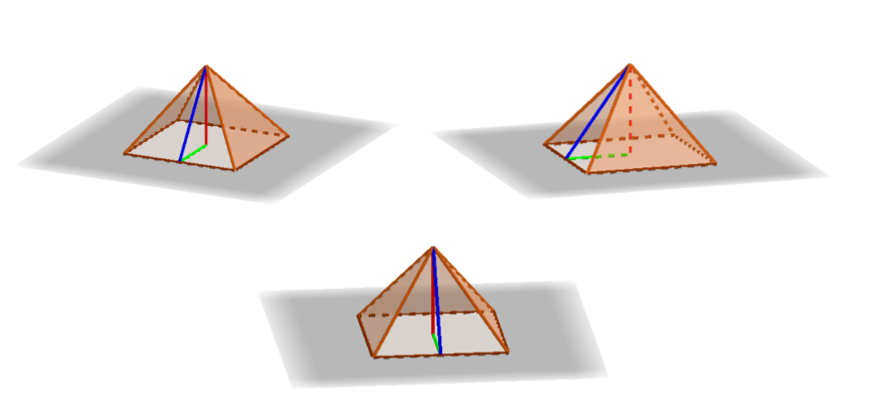
¿Qué características tiene la altura de una pirámide? ¿y en el caso de la pirámide regular cuadrangular? ¿Qué puede observarse respecto del punto de intersección de las diagonales de la base de la pirámide con la altura de la misma? 

¿Y la línea verde? ¿Podremos calcular su longitud? 

¿Qué podés decir de la línea azul? ¿Sobre qué figura geométrica está trazada? ¿Qué nombre recibe y qué características tiene? 

Podremos observar que las tres líneas de color forman una figura conocida. Clasifica la figura según sus lados y sus ángulos.

¿Qué diferencias y qué similitudes hay matemáticamente entre la línea roja y la azul? (La identificación de las similitudes y diferencias es indispensable para distinguir la altura del cuerpo y la altura de la figura.)

Ahora que trabajamos un poco más: ¿Se te ocurre alguna forma de calcular la longitud de la línea azul?

Seguí debatiendo con tus docentes para arribar o profundizar en recursos que te permitan el cálculo de esta medida.

 

Hemos realizado un recorrido utilizando Google Earth. ¿Te interesaría ir más allá del planeta Tierra? 

Esta información te ayudará:

5-BIBLIOGRAFÍA:

BARBERA GREGORI, E. – (1996)  : “Estimación estratégica: la matemática como ciencia inexacta ”. UNO Revista de Didáctica de las Matemáticas, 7, 125-134. GRAO. España.

BUZAI, G. – (2006) Geografía y Sistemas de Información Geográfica- Evolución teórico-metodológica hacia campos emergentes – Universidad Nacional de Luján. Recuperado en: http://observatoriogeograficoamericalatina.org.mx/egal13/Nuevastecnologias/Sig/01.pdf

Hay matemáticas en las principales aplicaciones de Google. Agencia Ibero Americana para la Difusión de la Ciencia y Tecnología.(2012, Mayo 18) Recuperado en: https://www.dicyt.com/noticias/hay-matematicas-en-las-principales-aplicaciones-de-google

Itzcovich, H. (2012) La Matemática escolar: Las prácticas de enseñanza en el aula, Buenos Aires, Aique.

Ministerio de Educación Ciencia y Tecnología de la Nación. (2007). Matemática: Leer, escribir y argumentar en Matemática, 7. Docentes. Buenos Aires, Argentina.

Ministerio de Educación Ciencia y Tecnología de la Nación. (2007). Matemática: Leer, escribir y argumentar en Matemática, 7. Alumnos. Buenos Aires, Argentina.

Ministerio de Educación, Ciencia y Tecnología de la Nación (2006). Núcleos de Aprendizajes Prioritarios 3er ciclo EGB / Nivel Medio. Matemática. Buenos Aires, Argentina.

 

Agradecemos la colaboración de la Profesora Mariela Pagani, miembro del Equipo Pedagógico de Educación Primaria.

 

Seguimos trabajando junto a ustedes. ¡Un afectuoso saludo!

Subsecretaría de Educación Primaria.