Acción Formativa Nº 114: “Patrones triangulares”

1- INTRODUCCIÓN:

Dando continuidad al trabajo que veníamos realizando compartimos con ustedes esta nueva publicación. En esta oportunidad le dedicaremos un espacio a la Geometría, especialmente para acompañarlas y acompañarlos en el  abordaje de problemas geométricos vinculados a los triángulos que posibiliten a las chicas y chicos de 5° grado de Educación Primaria construir nuevos saberes.

Les propondremos, en esta ocasión, una posible secuencia para el abordaje del objeto geométrico “triángulo”, de sus características y clasificación según sus lados y sus ángulos.

Esperamos que el presente material sea de suma utilidad para acompañar el trabajo áulico que será enriquecido con los aportes de todas y todos ustedes, docentes de Nivel Primario.

 

Prof. Ubaldo López

Subsecretaría de Educación Primaria.

 

2- RECORDAMOS ALGUNOS ACUERDOS:

Como se propone en los Núcleos de Aprendizajes Prioritarios (MECyT, 2006, pp. 17-20) correspondiente al Segundo Ciclo del Nivel Primario, en la escuela se deben proponer situaciones que requieran reconocer, copiar y construir triángulos; describirlos  y compararlos, con el fin de realizar una clasificación de los mismos explicitando las propiedades de sus lados, de sus ángulos y los criterios utilizados.

Por esto, tal como se expresa en Cuadernos para el Aula 5 (MECyT, 2007, p. 136), “En 5º año/grado trabajaremos para que los alumnos sistematicen las propiedades que seguramente han explorado en años anteriores, las de los lados y ángulos de triángulos…”.

3- COMPARTIMOS ALGUNOS SABERES:

En paralelo con el estudio de los contenidos del Eje “Número y Operaciones”, será importante abordar también conocimientos referidos al Eje “Geometría y Medida”, en el cual se incluye el estudio de los objetos geométricos, es decir las formas de dos y tres dimensiones.

Para habilitar discusiones sobre los saberes que se pondrán en juego en esta acción, comenzaremos planteando algunos interrogantes para reflexionar:

 

¿Qué nociones deben construir las niñas y los niños cuando abordamos este Eje?

Como se expresa en la Acción Formativa Nº 101 “Un mundo lleno de formas”, disponible en el Campus Educativo de Santa Fe, “En Geometría, sin lugar a dudas, un lugar de ineludible abordaje tiene que ver con las figuras de dos y tres dimensiones o, como en la mayoría de los textos aparece, las figuras y los cuerpos geométricos”.

Si bien uno de los objetivos de la enseñanza de la Geometría es el estudio de las propiedades de las formas geométricas, también debemos hacer hincapié en el modo de pensar geométrico, es decir, que las chicas y los chicos se apoyen en las propiedades de las formas conocidas para continuar construyendo más conocimiento.

Por lo antes mencionado, en la presente Acción Formativa pretendemos que las chicas y los chicos de 5º grado enriquezcan los conocimientos construidos durante el Primer Ciclo de la escuela primaria y 4º grado sobre triángulos,  sustentados en ciertas propiedades “observables” para poder clasificarlos a partir de diferentes criterios.

Será indispensable para el abordaje de la presente secuencia conocer las concepciones de las y los estudiantes en torno a ciertos conceptos y propiedades de los triángulos.

¿A qué nos referimos cuando hacemos alusión a dimensiones en una figura?

Las formas geométricas no son todas iguales. Una de las cuestiones que permite distinguirlas, clasificarlas y describirlas es la dimensión. Cuando nos referimos a este término, nos remitimos al lugar geométrico donde esa forma existe. Por ejemplo: 

– un punto es una figura sin dimensión (adimensional), no tiene ninguna dirección; 

– una recta tiene una dimensión (unidimensional), una dirección que nos permite indicar dos sentidos;

– una figura plana tiene dos dimensiones (bidimensional), es aquella que está contenida en un plano;

– un cuerpo es una figura de tres dimensiones (tridimensional), no está contenido en un plano.

En esta Acción Formativa estudiaremos una de las figuras bidimensionales, aquella delimitada por tres líneas rectas.

¿Podemos vincular las figuras de dos dimensiones con los objetos cotidianos? 

En Segundo Ciclo es imprescindible que las chicas y los chicos comprendan que los objetos geométricos no existen en la realidad, todo lo que se observa son objetos perceptibles que nos ayudan a realizar una representación mental de los objetos geométricos de acuerdo a las características de los mismos.

Al respecto, Godino expresa que:

“debemos tener claro que cuando hablamos de “figuras o formas geométricas” no nos referimos a ninguna clase de objetos perceptibles, aunque ciertamente los dibujos, imágenes y materializaciones concretas son, al menos en los primeros niveles del aprendizaje, la razón de ser del lenguaje geométrico y el apoyo intuitivo para la formulación de conjeturas sobre las relaciones entre las entidades y propiedades geométricas.” (Godino, J D,  p 457) 

Para ello consideramos que es necesario plantear problemas que permitan comprender el carácter abstracto de la Geometría. En relación a esto, Mónica Urquiza sostiene que estos problemas deben permitir la interacción de cada estudiante con los objetos que no pertenecen al espacio físico, sino a un espacio conceptualizado representado por las figuras – dibujos. (2011, p. 131)

Al momento de abordar las figuras de dos dimensiones será necesario tener presente que los objetos cotidianos poseen tres dimensiones. Por lo tanto, las propuestas sobre las mismas deberán relacionarse con formas que sean parte de dichos objetos. Por ejemplo, un triángulo podría relacionarse con una de las caras de una pirámide de Egipto y no con la pirámide en su totalidad.

¿Cómo se define al objeto geométrico denominado triángulo?

Como ya sabemos, el triángulo es el polígono de menor número de lados. (Entendemos por polígono a una porción de un plano delimitada por líneas rectas).

En diversos textos, se define como:

– “Es un polígono de tres lados, es decir, una porción de plano limitada por tres segmentos unidos, dos a dos, por sus extremos”. (Godino, J D, 2002, p. 465) 

– En Geometría sin esfuerzo, de Sánchez (1983), se tiene como definición y características de un triángulo: “Se entiende por triángulo una porción de plano limitada por tres rectas que se cortan dos a dos. Se representa por el símbolo ∆”. (Barroso Campos, R, 2000, p. 288) 

– En el Diccionario de la Lengua Española, de la Real Academia Española (1992), el triángulo tiene tres acepciones. La segunda es la que nos interesa “2. m. Geom. Figura formada por tres rectas que se cortan mutuamente formando tres ángulos”. (Barroso Campos, R, 2000, p. 288)  http://funes.uniandes.edu.co/21875/1/Barroso2000El.pdf 

 

Estas definiciones poseen un grado importante de complejidad. No obstante, como el proceso de aprendizaje implica construir nociones y acercarse gradualmente al objeto geométrico, las y los estudiantes de 5º grado podrán acceder a una definición más descriptiva como la siguiente: “un tri-ángulo o un tri-látero es un polígono que tiene tres ángulos y tres lados”. 

¿Qué y cómo abordar triángulos?

Los saberes construídos en el Primer Ciclo acerca de los triángulos se irán enriqueciendo con lo trabajado en 4° grado.

Una de las primeras líneas de acción para trabajar con las chicas y los chicos de 5º grado estará vinculada a la condición necesaria que deben cumplir las longitudes de los lados de un triángulo. Es decir, será imprescindible reflexionar acerca de si siempre será posible construir un triángulo dadas las longitudes de tres segmentos (lados).

Es probable que la respuesta por parte de las y los estudiantes sea afirmativa, por lo que será tarea del docente plantear situaciones problemáticas y habilitar espacios posteriores de discusión para descartar dicha conjetura.

Otra de las acciones, estará vinculada a la clasificación de los triángulos. Dada una variedad de triángulos, lo verdaderamente valioso será que las chicas y los chicos propongan criterios y clasifiquen en consecuencia. Aquí surgirán diversas posibilidades al respecto y será importante generar un espacio para compartir las ideas. Algunos criterios de agrupación podrán ser: por tamaño, por color, por las formas de sus ángulos, por las longitudes de los lados… y en estos dos últimos es donde nos vamos a detener.

Como docentes, debemos reflexionar acerca de: ¿Qué implica realizar una clasificación de los triángulos según sus lados? 

En diversos textos escolares encontramos que para el abordaje de la clasificación de los triángulos según sus lados, algunos de ellos no especifican el criterio y otros expresan que se ha de tener en cuenta la longitud de los lados. Es decir, por ejemplo, si tres de sus lados tienen la misma medida esos triángulos se llaman equiláteros; si dos de sus lados tienen la misma medida, esos triángulos se llaman isósceles y si todos los lados tienen distintas medidas esos triángulos se llaman escalenos.

Creemos que será importante detenerse en la definición de triángulo isósceles ya que en muchas oportunidades se lo define como aquel que tiene dos lados congruentes y uno desigual. Consideramos que esta definición imposibilita establecer relaciones entre los triángulos isósceles y equiláteros, teniendo en cuenta que todo triángulo equilátero es a su vez isósceles. 

Para evitar que esto ocurra, sería conveniente plantear una propuesta teniendo en cuenta el siguiente criterio de clasificación de triángulos: según  el número de lados congruentes. De esta manera, les resultaría más fácil a las y a los estudiantes definir a los triángulos equiláteros como aquellos que no tienen  lados congruentes; los triángulos isósceles como lo que tienen dos lados congruentes y los triángulos escalenos como aquellos que tienen sus tres lados no congruentes.

Para continuar reflexionando… ¿Qué implica realizar una clasificación de los triángulos según sus ángulos? ¿Para realizar dicha clasificación tenemos en cuenta la congruencia de las amplitudes de sus ángulos o los tipos de ángulos que determinan según su amplitud?

Es común leer en libros escolares, que una posibilidad para clasificar los triángulos es teniendo en cuenta la amplitud de los ángulos. Es decir, al tipo de ángulos que los forman: si todos sus ángulos son agudos, esos triángulos se llaman acutángulos; si uno de sus ángulos es recto, esos triángulos se llaman rectángulos y si uno de esos ángulos es obtuso, esos triángulos se llaman obtusángulos.

A lo explicitado en el párrafo anterior, la idea de clasificarlos según la cantidad de ángulos congruentes, habilitará además el desarrollo de las propiedades que vinculan los lados y ángulos interiores de los triángulos. Las y los estudiantes podrían, de esta manera, deducir que los triángulos equiláteros tienen los tres ángulos congruentes (equiángulos), los triángulos isósceles tienen dos ángulos congruentes y los triángulos escalenos no tienen ángulos congruentes.

4- RESOLVEMOS, CREAMOS, PROPONEMOS:

En la actualidad muchos dispositivos electrónicos existentes, como las tablets y los celulares, nos brindan el acceso a información del mundo, nos permiten comunicarnos, acortar distancias, registrar momentos importantes de nuestras vidas a través de fotos, videos…  Además son herramientas utilizadas por muchas personas para trabajar, estudiar, ofrecer servicios, etc. 

Para resguardar nuestra privacidad, es necesario proteger la información contenida en los mismos. 

Propondremos comenzar la acción invitando a las chicas y a los chicos a imaginar que son analistas de códigos. Desde ese lugar:

¿Cómo podemos hacer para mantener segura la información de un teléfono  celular o de una tablet?

Al momento de configurar estos dispositivos, el sistema operativo de los mismos nos suele dar varias opciones para bloquearlos de modo que nadie pueda acceder a ellos. 

Este interrogante inicial será pertinente para abordar con las chicas y los chicos cuestiones referidas al resguardo de información personal a través de las siguientes preguntas:

– ¿Por qué será importante bloquear un dispositivo electrónico?

– ¿Qué tipos de bloqueos conocen? (patrón, código pin o contraseña y huella dactilar)

– ¿Cuál o cuáles consideran que son más seguros? ¿Por qué?

Para profundizar sobre cómo proteger nuestros dispositivos electrónicos personales te invitamos a visitar el siguiente sitio, disponible en: :https://www.argentina.gob.ar/justicia/convosenlaweb/situaciones/como-proteger-el-celular-de-robos-o-perdidas

Ingresando al mundo de la Geometría…

ACTIVIDAD 1. 

a) Observá la siguiente imagen de pantalla de bloqueo y tratá de reproducirla en una hoja de tu carpeta.

b) ¿Qué tuviste en cuenta a la hora de reproducir esa imagen en tu hoja? 

(Algunas respuestas posibles de las y los estudiantes pueden ser: son 9 puntos o círculos que  forman un cuadrado, están alineados en forma vertical y horizontal, etc. Será pertinente intervenir en el caso que las respuestas sean incompletas. Es importante que las chicas y los chicos puedan notar que los puntos consecutivos alineados están a la misma distancia entre sí).

ACTIVIDAD 2. 

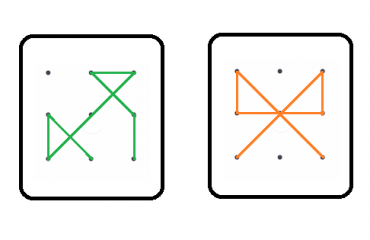
Sabiendo que algunos posibles patrones de bloqueo para un celular o tablet pueden ser los siguientes:

a. ¿Qué ventajas y desventajas puede tener usar un patrón como los anteriores? 

b. ¿Se podrán crear patrones más simples o más complejos? 

c. ¿Qué formas (polígonos) tienen en común los patrones de la imagen? Justificá.

d. Si tuvieras que idear un patrón para este 2023, ¿cómo sería? Dibujalo en tu pantalla creada en la hoja.

ACTIVIDAD 3

Los diseñadores de códigos se dieron cuenta que no es posible realizar un único polígono como patrón de bloqueo…. ¡Porque no se cierra!

Suponiendo que en un futuro, una nueva versión sí los admita. Ante esta posibilidad: Ana está pensando en diseñar un triángulo como posible patrón de bloqueo del celular de su mamá. ¿Qué características tendrá dicho patrón? ¿Cómo podría ser? ¿Existe una única posibilidad? Justificá tus respuestas.   

¡Cuantos más puntos, mejor!

Trabajamos con geoplanos.

Al momento de crear el patrón, cada docente podría presentar a las chicas y los chicos un geoplano para que puedan realizarlo. El mismo es un recurso didáctico consistente en un tablero cuadrado (aunque puede ser también de cualquier forma), de material resistente. Su interior contiene una cuadrícula realizada con clavos, tarugos de madera u otro elemento donde se colocan gomas elásticas de colores que permiten formar las figuras geométricas que se deseen.

Observación: se podría proponer la construcción del geoplano, en forma conjunta con Educación Tecnológica.

También se puede recurrir a la utilización de un geoplano digital que se encuentra disponible en:  http://didacticaespecializada.com.mx/multimedia/geoplano/ 

Para la puesta en común, se podría realizar la cuadrilla en un papel afiche, usar una plancha de corcho con chinches, o bien, el geoplano para que se puedan exponer las distintas producciones. Una vez compartidas, deberán copiar dichas formas en una hoja de la carpeta que contenga puntos que simule el recurso utilizado. A modo de ejemplo:

ACTIVIDAD 4. 

Observando lo realizado, te invitamos a responder: ¿Todos los triángulos son congruentes? ¿Por qué?

Es probable que la respuesta por parte de las chicas y los chicos sea “no”. Podrán expresar que: “unos triángulos tienen algunos lados iguales”, “otros triángulos son más chiquitos”, “algunos triángulos parecen escuadras”, etc. También puede ocurrir que usen un vocabulario más específico o que los clasifiquen porque ya lo desarrollaron en 4to grado.

Ya sabemos que entre los triángulos representados no estarán incluidos los triángulos equiláteros ya que el recurso del geoplano no permite su construcción. Además, puede ocurrir que falten otros. Por este motivo, a través de preguntas, podrá solicitarse pensar otras construcciones, argumentando sobre la viabilidad de representación: ¿Hay triángulos que tengan todos sus lados de igual longitud? ¿Es posible construir en el geoplano un triángulo cuyos tres lados sean congruentes? ¿Y en una hoja cualquiera? ¿Hay triángulos que posean algún ángulo obtuso? ¿Será posible construir un triángulo que posea un ángulo recto y dos lados congruentes? ¿Y un ángulo recto y sus tres lados de diferente longitud? 

Un registro en el pizarrón de todas las posibilidades y respuestas que vayan formulando las y los estudiantes podrá convertirse en un gran recurso para organizar la discusión posterior.

ACTIVIDAD 5. 

Si tuvieras que agrupar por semejanzas y separar por diferencias, ¿qué tendrías en cuenta para hacerlo?

Frente a esta propuesta, las chicas y los chicos podrán utilizar diferentes criterios para agruparlos, ya que las concepciones que tienen sobre las representaciones de los triángulos suelen ser variadas y probablemente puedan estar asociadas a triángulos acutángulos y, en particular, a triángulos isósceles. 

Esta actividad abrirá camino para el debate y la argumentación sobre estas representaciones, esbozando algunas características que podrán derivar en la posterior clasificación, valorando e interpelando las explicaciones y orientando la puesta en común hasta arribar a los siguientes criterios: según el número de lados congruentes, por un lado, y según los tipos de ángulos interiores, por otro.

Al momento de institucionalizar lo realizado y luego de escuchar las voces de las chicas y los chicos, serán las y los docentes quienes se encargarán de atribuirle nombre al triángulo que tiene, por ejemplo, tres lados congruentes, al que tiene dos y al que no los tiene. De igual forma se procederá con la clasificación según los ángulos.

ACTIVIDAD 6. 

TODO MEZCLADO

1. a) Si la mamá de Ana tuviera un celular que tiene una pantalla para hacer patrones como se muestra en la figura:

Se puede acceder a la hoja imprimible en A4 haciendo clic en el siguiente enlace: https://docs.google.com/document/d/1KcUD9-hl8rAG_KYqr8tP62XMKT63T_xxvtLRv06U4h8/edit?usp=sharing

 

Representá cómo podría ser su patrón si se sabe que tiene la forma de:

         i) un triángulo rectángulo isósceles.

         ii) un triángulo escaleno obtusángulo.

         iii) un triángulo acutángulo equilátero.

b) En cada uno de los casos anteriores, analizá si existe la posibilidad de construir más de un triángulo de cada tipo y compará con los realizados por tus compañeras y compañeros. 

2. Para pensar… Mateo dice que la forma del patrón de desbloqueo de su celular es un triángulo isósceles equilátero. ¿Es cierto lo que dice? Justificá.

¡Seguimos trabajando juntas y juntos en este espacio!

5- BIBLIOGRAFÍA:  

– Alessi, A., Pagani, M. y Sequier, R. (2022).  Acción Formativa Nº 101: “Un mundo lleno de formas”. Campus Educativo de la Provincia de Santa Fe. https://campuseducativo.santafe.edu.ar/accion-formativa-n-101-un-mundo-lleno-de-formas/ 

– Barroso Campos, R. (2000). El proceso de definir en matemáticas. Un caso: el triángulo. Departamento de Didáctica de las Matemáticas. Universidad de Sevilla, España. http://funes.uniandes.edu.co/21875/1/Barroso2000El.pdf

– Ministerio de Educación, Ciencia y Tecnología de la Nación (2006). Núcleos de Aprendizajes Prioritarios. 2º ciclo EGB / Nivel Primario. Matemática. Buenos Aires, Argentina. https://www.educ.ar/recursos/132576/napeducacion-primaria-segundo-ciclo/download/inline 

– Ministerio de Educación, Ciencia y Tecnología de la Nación (2007). Cuadernos para el aula: Matemática 5. Buenos Aires, Argentina. http://www.bnm.me.gov.ar/giga1/documentos/EL001100.pdf  

– Godino, J. y Ruiz, F. (2002). Geometría y su Didáctica para Maestros. https://www.ugr.es/~jgodino/edumat-maestros/manual/4_Geometria.pdf 

– Urquiza, M. (2011). Geometría (129-148). En Castro, A… [et al.] (2011) Enseñar matemática: en la escuela primaria – Serie Respuestas. Tinta Fresca.

 

Agradecemos a Alejandro Alessi, Mariela Pagani, Lorena Rosati y Romina Sequier que redactaron la presente Acción Formativa y forman parte del Equipo Pedagógico de la Subsecretaría de Educación Primaria. 

¡Nos seguimos encontrando en este espacio!

Equipo Pedagógico

Subsecretaría de Educación Primaria