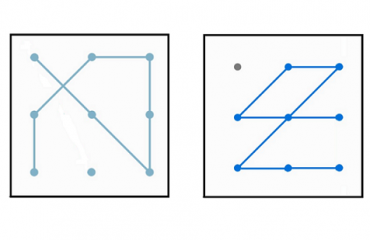
Acción Formativa N° 120 : “Los cuadrilados”

 

1- INTRODUCCIÓN:

Queremos invitarlas e invitarlos en esta oportunidad, a la lectura de una nueva propuesta para continuar acompañando la construcción de los saberes de las chicas y de los chicos de 5º grado. 

Ponemos a disposición de todas y todos ustedes, docentes de la Provincia de Santa Fe, la presente secuencia para abordar las características de los cuadriláteros y posibles clasificaciones de los mismos.

Esperamos que puedan disfrutar de la propuesta, ponerla en práctica,  enriquecerla y por qué no, ampliarla. Sigamos convirtiendo el aula en ese lugar donde es posible la construcción de saberes matemáticos.

 

Prof. Ubaldo López

Subsecretaría de Educación Primaria.

2- RECORDAMOS ALGUNOS ACUERDOS:

Para 4º, 5º y 6º grado, la escuela deberá ofrecer diferentes situaciones de enseñanza que promuevan en las y los estudiantes: “El reconocimiento y la clasificación de figuras y cuerpos geométricos a partir de sus propiedades en la resolución de problemas”. Así se establece en los Núcleos de Aprendizajes Prioritarios correspondiente al Segundo Ciclo del Nivel Primario (MECyT, 2006, pp. 12-13).

Por lo antes mencionado, particularmente en 5º grado se deberán proponer diversas situaciones que impliquen describir, reconocer y comparar cuadriláteros. Además, clasificarlos de diferentes formas explicitando los criterios utilizados: teniendo en cuenta la longitud y posición relativa de sus lados, la perpendicularidad (o no) de las  diagonales, la amplitud de sus ángulos…

La utilización de recursos didácticos, particularmente, aquellos asociados a entornos digitales ofrece la posibilidad de abordar los contenidos expresados en los Núcleos de Aprendizajes Prioritarios (MECCyT, 2018, p. 18) de Educación Digital, Programación y Robótica ya que en el mismo se establece que durante el Segundo Ciclo, la escuela ofrecerá situaciones de enseñanza que promuevan en las alumnas y los alumnos: “El trabajo colaborativo y solidario mediado por TIC para la resolución de problemas, favoreciendo el intercambio de ideas, y la comunicación de forma clara y secuenciada de las estrategias de solución”.

 

3- COMPARTIMOS ALGUNOS SABERES:

Como ya sabemos, desde el Primer Ciclo se producen los primeros acercamientos de las niñas y de los niños a las figuras de dos dimensiones a partir de un trabajo que involucra la exploración. Con el fin de que se apropien progresivamente de las propiedades de estas y pretendiendo avanzar tanto en la construcción de conocimientos como así también en la elaboración de argumentos, a lo largo del Segundo Ciclo será necesario plantear propuestas áulicas que permitan que luego de un trabajo exploratorio, las chicas y los chicos puedan establecer si las afirmaciones o conjeturas elaboradas son ciertas o no, sin la necesidad de apelar a la constatación experimental.

Tal como se expresa en Cuadernos para el Aula de 5° grado, es importante recordar que ciertas propiedades no son “observables” a partir de un dibujo, dado que lo que cada alumno “ve” está en relación directa con los conocimientos que posee, por lo que será imprescindible el desarrollo de cierta actividad intelectual que “las hagan evidentes”. (MECyT, 2007, pp. 135-136) 

Con el fin de indagar cuestiones acerca de: ¿qué nociones deben construir las niñas y los niños cuando abordamos el Eje “Geometría y medida”?, ¿a qué nos referimos cuando hacemos alusión a dimensiones en una figura? y ¿podemos vincular las figuras de dos dimensiones con los objetos cotidianos?, les proponemos visitar la Acción Formativa N° 114 titulada “Patrones triangulares”, disponible en: https://campuseducativo.santafe.edu.ar/accion-formativa-no-114-patrones-triangulares/ 

 

Nos adentramos en el mundo de los polígonos de cuatro lados y cuatro ángulos…

¿Cómo se podría denominar al objeto geométrico formado por cuatro lados y cuatro ángulos?

Si esta pregunta la compartiéramos con las y los estudiantes de 5º grado, posiblemente respondan de forma inmediata “cuadrado o rectángulo”. Es decir, lo asocian a aquellas figuras más “utilizadas” en el Primer Ciclo que cumplen con las condiciones dadas y, de ser así, allí se hace presente un interrogante interesante: ¿solamente tenemos que abordar rectángulos y cuadrados en Primer Ciclo en relación a los polígonos de cuatro lados y cuatro ángulos?. Otras y otros, en cambio, podrán decir “cuadrilátero” porque lo leyeron en libros de textos escolares, lo escucharon en años anteriores, o bien, “cuadrángulo” porque pueden suponer que si al polígono que tiene tres lados y tres ángulos se lo llama triángulo, al que tiene cuatro lados y cuatro ángulos se lo llamará cuadrángulo. Entonces, ¿cuál será el término adecuado? 

Ambos términos son correctos ya que al polígono de cuatro lados y cuatro ángulos se lo puede denominar como cuadrilátero o cuadrángulo. En caso de querer acercarse y construir una posible definición, sugerimos que junto con las chicas y los chicos se arribe a un concepto de tipo descriptivo tal como: “un cuadrilátero o un cuadrángulo es un polígono de cuatro lados y cuatro ángulos”. Vale aclarar que, así como es común denominar a las figuras de tres lados triángulos y no triláteros; es común llamar a las figuras de cuatro lados cuadriláteros y no cuadrángulos. Sin embargo, debemos tener en cuenta que lo común, no necesariamente implica "adecuado", "correcto" o "inmodificable".

Para ampliar cuestiones vinculadas al tratamiento de las formas en Primer Ciclo y encontrar una posible respuesta a cómo se denominan los objetos geométricos formados por cuatro lados y cuatro ángulos, las y los invitamos a leer la Acción Formativa Nº 101: “Un mundo lleno de formas”, disponible en:

https://campuseducativo.santafe.edu.ar/accion-formativa-n-101-un-mundo-lleno-de-formas/ 

Es importante reconocer en estas figuras un nuevo elemento: la diagonal. Si bien en años anteriores quizás dicha noción fue nombrada, en 5° grado será pertinente que las y los estudiantes puedan construir nociones en relación a su definición. Tal vez, una manera de ayudar a las chicas y chicos sea a partir de preguntas tales como, ¿por qué los triángulos no tienen diagonales y el resto de los polígonos si? ¿Qué característica tiene esa línea o segmento para distinguirse de los lados? Luego de un espacio de discusión, las chicas y los chicos podrán indicar que una diagonal es “la línea recta o segmento que no es un lado y une dos vértices”.

En esta Acción Formativa, intentaremos ampliar y/o acompañar las propuestas presentes en los diversos textos escolares referidas a la clasificación de cuadriláteros, poniendo énfasis en la importancia de dar lugar a las chicas y a los chicos, a utilizar criterios propios, ya que estos mismos podrán ser luego objeto de discusión dando lugar al reconocimiento de propiedades y a su clasificación convencional. 

Entonces… ¿Qué criterios podrán surgir al momento de proponer clasificar diversos cuadriláteros? 

A partir de un conjunto de representaciones dedistintos tipos de cuadriláteros, variados criterios de clasificación podrán surgir por parte de las chicas y de los chicos. Algunos de ellos estarían vinculados quizás con el tamaño o con su relación a cuadriláteros conocidos (los conozco, no los conozco). Si ya se abordó con anterioridad la clasificación de triángulos, otra posibilidad podría ser que extiendan dichos criterios a los cuadriláteros y pretendan clasificarlos según el número de lados congruentes o según el tipo de ángulos que poseen. 

Otro criterio podría estar vinculado a su forma. Lo interesante ahora será reflexionar acerca de… ¿qué significa clasificarlos por forma? ¿dónde ubicamos la mirada para clasificar a los cuadriláteros según la forma?  

Frente a este último interrogante, podrán hacer alusión a:

– Los ángulos. Una posible respuesta será que “hay cuadriláteros que tienen ángulos para adentro y otros que no”, lo que puede dar lugar a una primera clasificación y definición: los cuadriláteros que tienen “ángulos para adentro” se denominan cóncavos y los que no los tienen se denominan convexos. Será importante que las y los estudiantes con la guía de su docente puedan construir nociones en relación a la definición reflexionando sobre sus dichos acerca de ¿cuándo un ángulo de un cuadrilátero “parece estar para adentro” y cuándo “parece estar para afuera”? Esto permitirá establecer que un cuadrilátero es cóncavo cuando uno de sus ángulos tiene una amplitud mayor a 180º y convexo cuando todas las amplitudes de sus ángulos son menores a 180º. 

– La posición de los lados. Ante este criterio podrán indicar utilizando sus manos que algunos lados de los cuadriláteros “son así”, haciendo referencia al paralelismo de sus lados. 

Siendo probable que este último criterio de clasificación no surja, será pertinente proponer a las chicas y a los chicos que piensen en un nuevo criterio que no se encuentre relacionado con la congruencia de los lados, sino a la posición de los mismos. De esta manera, nos estaremos aproximando a la clasificación convencional de los cuadriláteros:

 

Los cuadriláteros pueden clasificarse según si tienen: – Ningún par de lados paralelos. Se denominan trapezoides. – Un par de lados paralelos. Se denominan trapecios. – Dos pares de lados paralelos. Se denominan  paralelogramos.

 

 

 

Nos parece muy interesante reflexionar sobre el criterio de paralelismo de lados, ya que dicho criterio de clasificación permite la posibilidad de establecer relaciones entre los diversos tipos de cuadriláteros. Por ejemplo: todo romboide es trapezoide; todo cuadrado es paralelogramo, etc. (Vale aclarar que en algunos sitios de internet correspondientes a otros países, al paralelogramo propiamente dicho se lo denomina romboide).

En todos los casos, será indispensable que se brinden momentos y espacios de validación donde las chicas y los chicos puedan compartir los criterios elegidos, sean capaces de fundamentar sus elecciones y analizar la pertinencia (o no) de los mismos. 

4- RESOLVEMOS, CREAMOS, PROPONEMOS:

Continuaremos trabajando con el contexto propuesto en la Acción Formativa Nº 114 denominada “Patrones triangulares” con la diferencia que, en esta oportunidad, las figuras a representar serán cuadriláteros.

¡Comenzamos! 

ACTIVIDAD 1 

¡Aparecieron más patrones de bloqueo de celular! 

Observá los patrones y realizá las siguientes actividades:

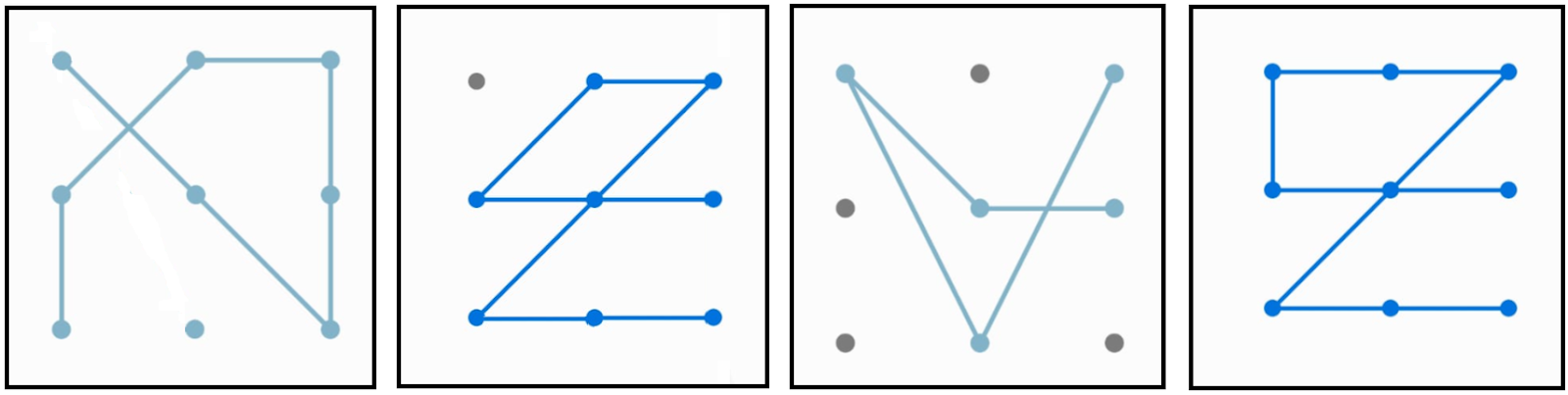
a. Pinten los polígonos que quedaron determinados en el trazado de los patrones. ¿Qué tienen en común? ¿Qué nombre recibe el conjunto de todos ellos? ¿Por qué? 

Se espera que, ante esta actividad, las chicas y los chicos se introduzcan en el mundo de los cuadriláteros. Será en este momento donde, en forma conjunta, se construirán nociones vinculadas a la definición de cuadriláteros y de esta manera se podrá analizar la posibilidad de denominarlos cuadrángulos.

 

b. A Ana le pidieron que represente los cuatro cuadriláteros en un geoplano o en una hoja de carpeta y que con ellos arme dos grupos teniendo en cuenta algún criterio. ¿Cómo los habrá representado? ¿De qué forma los habrá agrupado? ¿Qué habrá tenido en cuenta para hacerlo? 

Respecto a la representación a realizar, se deberá indicar a las chicas y a los chicos que lo importante será mantener la forma de los cuadriláteros, es decir, que las representaciones tengan la mayor proximidad posible con las de la imagen. Esta actividad permitirá a las y los estudiantes pensar cómo realizarlas y posteriormente tomar decisiones al respecto.

Una vez efectuadas las representaciones y agrupamientos que pudo haber realizado Ana, será importante brindar un espacio de trabajo donde las chicas y los chicos puedan expresar lo realizado al respecto.

Si en la clase alguna chica o algún chico expresa que Ana los clasificó teniendo en cuenta los ángulos de las figuras y encontró que uno de los cuadriláteros tiene un ángulo mayor a 180º y los otros no, se pondrá en discusión dicho criterio de clasificación y se omitirá la actividad del ítem c. (Caso contrario, con el fin de tensionar la noción de concavidad, se continuará con la actividad c y se institucionalizará finalizada la misma).

De manera colectiva se podrá arribar a una primera institucionalización:

 

Los cuadriláteros que tienen un ángulo interior mayor a 180° se denominan CÓNCAVOS. Los cuadriláteros que tienen todos sus ángulos menores a 180° se denominan CONVEXOS.

 

 

 

Además, será un buen momento para reflexionar si es posible agrupar de esta manera patrones  que contengan polígonos triángulares. 

 

c. Ana los clasificó de esta manera: 

 

 ¿Qué habrá tenido en cuenta para hacerlo? 

 

d. Si tuvieras que representar en un geoplano o en una hoja punteada  dos cuadriláteros convexos que puedan estar contenidos en dos patrones distintos, ¿cómo serían? ¿Recordás sus nombres específicos? (Observación: el geoplano a utilizar podrá ser digital o convencional)

Con esta actividad se intenta mostrar la gran variedad de representaciones posibles de cuadriláteros para luego ser compartidos junto con el resto de la clase. 

La primera pregunta habilitará la caracterización de las distintas representaciones. Por ejemplo: podrán indicar que tiene dos lados paralelos, cuatro lados iguales (congruentes), todos los ángulos distintos, cuatro ángulos rectos, dos ángulos agudos y dos obtusos, etc. 

Puede ocurrir que entre los cuadriláteros representados y caracterizados no estén incluidos todos los que son necesarios para realizar la clasificación según el paralelismo de lados. Por este motivo, se podrá solicitar a través de preguntas, imaginar otras posibilidades, argumentando sobre la viabilidad de representación: ¿Hay cuadriláteros que tengan todos sus lados de igual longitud? ¿Será posible representar un cuadrilátero que posea tres ángulos obtusos? ¿Hay cuadriláteros que posean dos pares de lados congruentes? ¿Será posible construir un cuadrilátero que posea dos ángulos rectos y dos lados paralelos?, etc.

La segunda pregunta brindará la posibilidad de atribuirle un nombre a cada cuadrilátero representado si es que lo recuerdan. Caso contrario, será la o el docente quien lo indique.

Sugerimos que dichas caracterizaciones y denominaciones sean registradas en un afiche para luego ser utilizadas como recurso en actividades posteriores.

ACTIVIDAD 2

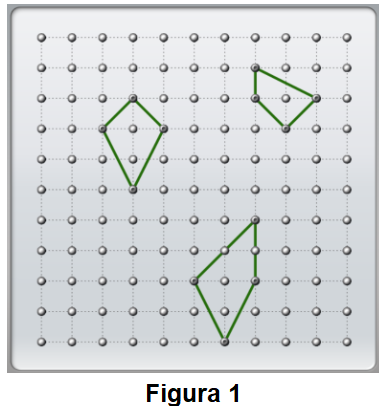
a. En el grado de Ana se representaron los siguientes cuadriláteros en un geoplano. Si tuvieras que agruparlos de alguna manera, ¿Cómo lo harías? ¿Qué tendrías en cuenta?

El propósito de esta actividad es que las chicas y los chicos puedan clasificar todos los cuadriláteros que observan en la imagen de acuerdo a diferentes criterios que sean propuestos por ellas y por ellos. Aquí surgirán diversas posibilidades al respecto y será importante generar un espacio para compartir las ideas. 

Podrán aparecer criterios vinculados con la forma de los ángulos, con la congruencia  de los lados, con el tamaño, etc. Si bien son criterios válidos, será oportuno incorporar, en caso de que no surja por parte de las chicas y de los chicos, una actividad que habilite a la clasificación de los cuadriláteros considerando como criterio de clasificación el paralelismo de los lados.

Si se obstaculice la realización de la clasificación, se podrá invitar a las chicas y a los chicos a participar de un juego de adivinación con dichos cuadriláteros, cuya intencionalidad didáctica será la apertura de un análisis descriptivo de las figuras, permitiendo el uso de vocabulario específico que luego facilitará la elección de criterios de clasificación. Observación: el juego consiste en elegir una de las figuras sin que el resto sepa de cuál se trata y a partir de preguntas, que solo podrán ser respondidas por Sí o por No, adivinar qué figura es.  

Por lo antes mencionado, podremos continuar proponiendo:

b. Si tuvieras que pensar en un criterio que involucre a los lados pero no a su congruencia ni longitud, ¿Cuál podría ser ese criterio? ¿Cómo quedarían  agrupados los cuadriláteros anteriores?

Esta actividad permitirá que además de la enunciación de criterios que involucran la congruencia de lados, de ángulos, sus tipos, etc., puedan identificar otra característica de los cuadriláteros, en este caso, el paralelismo de lados.

Es muy posible que las chicas y los chicos expresen que algunos cuadriláteros tienen lados paralelos y otros no. Si bien dicha afirmación sobre el paralelismo de los lados es válida, su abordaje requiere de un análisis más exhaustivo ya que se debe hacer referencia a la cantidad de pares de lados paralelos que poseen los diferentes cuadriláteros. Es por ello que la o el docente podrá intervenir presentando la siguiente actividad:

c. Pedro agrupó los cuadriláteros en estos tres grupos. ¿Qué criterio habrá utilizado? ¿Coincide con lo que pensaste?    

 

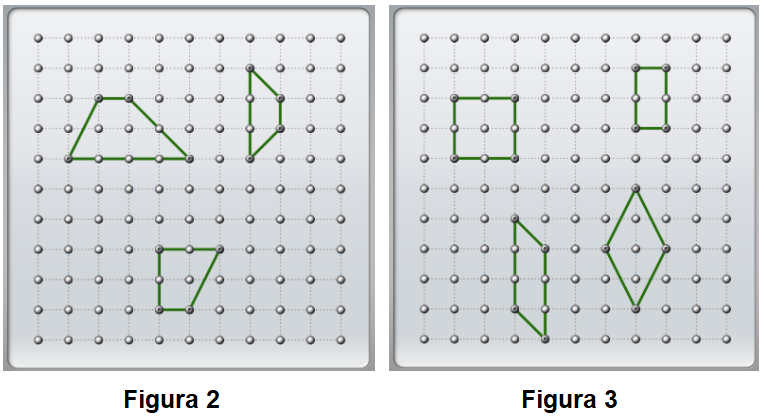
Se espera que de la observación y análisis de cada subgrupo de cuadriláteros se pueda arribar a la clasificación según el paralelismo de lados. Las y los estudiantes podrán expresar que “los de la figura 1 no tienen lados paralelos”,     “los cuadriláteros de la figura  2 tienen dos lados paralelos” y “los de la figura 3  tienen cuatro lados paralelos”. Ante esta última expresión se debería reflexionar si es posible o no la existencia de un cuadrilátero de cuatro lados paralelos.  

Será la o el docente quien indicará el nombre que recibe cada una de estas agrupaciones de cuadriláteros teniendo el cuenta la cantidad de PARES de lados paralelos. Ellos son: trapezoides, trapecios y paralelogramos.

Finalmente, las institucionalizaciones a las que se arribe serán reflejo de las construcciones evidenciadas en la clase. Algunas de ellas podrán ser:

 

Clasificación de los cuadriláteros según la cantidad de lados paralelos: – Los trapezoides no tienen lados paralelos. – Los trapecios tienen dos lados (un par)  paralelos. – Los paralelogramos tienen dos pares de lados paralelos.

 

ACTIVIDAD 3 

Si observás los paralelogramos representados en la actividad anterior notarás que no todos son iguales. ¿Qué características tiene cada uno de ellos?

Las y los estudiantes tendrán que focalizar la mirada en las características de los cuadriláteros que les permitan distinguirlos del resto. Podrán expresar que algunos cuadriláteros tienen los cuatro lados congruentes, otros que tienen cuatro ángulos rectos, otros que tienen los pares de lados paralelos congruentes, etc. Si anteriormente se han realizado registros en afiches o en carpetas, los mismos podrán ser utilizados en este momento. Luego de un espacio de análisis sobre estos cuadriláteros se podrá concluir, por ejemplo, que: el cuadrado tiene cuatro lados congruentes y cuatro ángulos rectos; el rombo tiene cuatro lados congruentes y dos pares de ángulos congruentes, etc.

En una secuencia posterior, se podrán abordar las características propias de los trapecios y de los trapezoides.

En 6° grado se deberá continuar con el trabajo de cuadriláteros estableciendo relaciones entre los mismos, por ejemplo: ¿todo cuadrado es rombo? ¿Todo rectángulo es cuadrado? ¿Algunos rombos son cuadrados?

Nótese que en toda la Acción Formativa  se presentó a los cuadriláteros en distintas posiciones. El geoplano es un recurso que permite visualizar la conservación de las propiedades de las formas independientemente de la posición.

MOMENTO PARA PONER EN ACCIÓN LO APRENDIDO

Les proponemos abordar algunas de las actividades seleccionadas del libro Carpeta de Matemática de 5° grado para poner a prueba los conocimientos construidos en la presente Acción Formativa sobre cuadriláteros, disponibles en: https://docs.google.com/document/d/1jfxfdRwBPomC_G4x1NEzOzFoVH_cyeWTSWK0PjCJA0o/edit?usp=sharing

ACTIVIDAD FINAL

Luego de resolver las actividades indicadas del libro, es momento de dar cuenta de lo aprendido. 

Lean los siete primeros ítems de la página 137 del libro de 5° grado. Observarán que en los mismos aparecen definiciones de cuadriláteros. ¿Coinciden con las que han construido? ¿En qué se parecen? ¿En qué se diferencian?

– Un cuadrilátero es una figura que tiene 4 lados.

– Un trapecio es un cuadrilátero que tiene dos lados no consecutivos paralelos. Los lados paralelos de los trapecios se llaman bases. El trapecio isósceles tiene dos lados iguales, el trapecio rectángulo tiene un lado perpendicular a las bases y el trapecio escaleno tiene todos sus lados y sus ángulos desiguales.

– Un paralelogramo es un cuadrilátero con los lados opuestos iguales y ambos pares de lados opuestos paralelos.

– Si un paralelogramo tiene los cuatro ángulos rectos, es un  rectángulo.

– Si un paralelogramo tiene los cuatro lados iguales, es un rombo.

– Si un rectángulo tiene los cuatro lados iguales, es un cuadrado. Por lo tanto, el cuadrado es, también, un rectángulo y un rombo. 

– Las diagonales de un cuadrilátero son los segmentos que unen sus vértices opuestos. En estas figuras, los segmentos BC y AD son las diagonales.

5- BIBLIOGRAFÍA:

Alessi, A., Pagani, M. y Sequier, R. (2022).  Acción Formativa Nº 101: “Un mundo lleno de formas”. Campus Educativo de la Provincia de Santa Fe. https://campuseducativo.santafe.edu.ar/accion-formativa-n-101-un-mundo-lleno-de-formas/ 

Ministerio de Educación, Cultura, Ciencia y Tecnología de la Nación (2018). Núcleos de Aprendizajes Prioritarios. Educación inicial Primaria y Secundaria. Educación digital, Programación y Robótica. Buenos Aires, Argentina. https://www.educ.ar/recursos/150123/nap-de-educacion-digital-programacion-y-robotica

Ministerio de Educación, Ciencia y Tecnología de la Nación (2007). Cuadernos para el aula: Matemática 5. Buenos Aires, Argentina. http://www.bnm.me.gov.ar/giga1/documentos/EL001100.pdf 

Ministerio de Educación, Ciencia y Tecnología de la Nación (2006). Núcleos de Aprendizajes Prioritarios. 2º ciclo EGB / Nivel Primario. Matemática. Buenos Aires, Argentina. https://www.educ.ar/recursos/132576/nap-educacion-primaria-segundo-ciclo/download/inline 

Nise, G. (2022). Cuaderno de Matemática 5. Sobre Ruedas. Nueva edición. Ciudad de Buenos Aires. Edelvives. Libros para Aprender. Edición Especial Ministerio de Educación de la Nación. 

 

Agradecemos a Alejandro Alessi, Mariela Pagani, Lorena Rosati y Romina Sequier que redactaron la presente Acción Formativa y forman parte del Equipo Pedagógico de la Subsecretaría de Educación Primaria. 

¡Nos seguimos encontrando en este espacio!

Equipo Pedagógico.

Subsecretaría de Educación Primaria