Acción Formativa N°97 “Triángulo múltiple”

1- INTRODUCCIÓN

En las Acciones Formativas anteriores para segundo grado planteamos posibles caminos para el abordaje de las operaciones del campo aditivo. Nos proponemos ahora, poner en discusión la diversidad de estrategias y de resoluciones que permiten algunas situaciones que corresponden al campo multiplicativo, mediante un recurso lúdico incorporado en las Acciones Formativas 86 y 95. Volvemos a mostrar cómo un mismo recurso, al que se le aplican algunas variantes, puede ser utilizado para diversas finalidades.

En esta secuencia se invita a encontrar y argumentar sobre diversos procedimientos para hallar la cantidad de puntos a partir de las discusiones sobre los registros y resoluciones. 

Como siempre, la presente secuencia no es la única posible, ni la mejor. La reflexión sobre la misma, la experticia docente, el conocimiento de los grupos a cargo y del contexto enriquecerá lo que aquí proponemos.

 

Las y los invitamos a leer la propuesta, a contextualizarla y a ponerla en práctica con sus grupos.

 

Prof. Ubaldo López

Subsecretaría de Educación Primaria

 

2- RECORDAMOS ALGUNOS ACUERDOS 

 

En los NAP correspondientes a primer ciclo de segundo grado (MEC y T, 2004, p. 16) se propone avanzar en el reconocimiento y uso de la multiplicación en el abordaje de situaciones que inviten a usar los distintos significados, a realizar cálculos y memorizar repertorios (dobles, triples). También se indica utilizar las propiedades de la adición y la multiplicación a la hora de calcular, explorar relaciones entre las operaciones argumentando sobre su validez y registrar y organizar datos en listas y tablas a partir de distintas informaciones.

 

En esta Acción Formativa se pondrá en tensión la resolución de situaciones que puedan ser resueltas por una multiplicación y que también permitan recurrir a otros procedimientos. Teniendo en cuenta que aunque no se haya construido el concepto, las niñas y los niños están en condiciones de resolver situaciones del campo multiplicativo mucho antes de que esta propuesta sea intencional.

 

3- COMPARTIMOS ALGUNOS SABERES

 

Entre los interrogantes que solemos hacernos a la hora de pensar la planificación en torno a la operatoria podemos enunciar: ¿Es necesario que las niñas y los niños aprendan primero a resolver las cuentas para resolver problemas? ¿Es indispensable que sepan las tablas para resolver problemas del campo multiplicativo? ¿Alcanza con resolver problemas? ¿Las tablas se tienen que memorizar? ¿Se pueden resolver problemas de multiplicación desde primer grado? ¿Qué proponer sobre multiplicación en cada uno de los grados? ¿Cómo abordar las propiedades de la multiplicación? ¿Cómo intervenir en la reversibilidad operatoria y en el vínculo con las otras operaciones? ¿Cómo propiciar la construcción del algoritmo? ¿Cuándo es el momento oportuno para dar a conocer los símbolos matemáticos? ¿Cuándo y cómo introducir el signo “x”? ¿Qué entendemos por “saber multiplicar”? ¿Cuándo decimos que una niña, un niño, sabe multiplicar? ¿Qué procedimientos de resolución potenciar? ¿Qué estrategias de cálculo? 

Algunos de estos interrogantes podremos abordarlos en la presente Acción Formativa, varios ya los venimos discutiendo en las anteriores y otros serán tema de próximas publicaciones.

Que las niñas y los niños se involucren en la producción de conocimiento matemático es una importante tarea que cada docente debe posibilitar. Para ello, como venimos sosteniendo en anteriores acciones formativas, un lugar interesante es la presentación de situaciones que se desprendan de un contexto que puede ser lúdico.

Continuamos insistiendo que se deben promover aquellos problemas que permitan la discusión de los “cómo” y no tanto de los “cuánto”. Es decir, que propongan interrogantes donde las niñas y los niños desplieguen sus argumentaciones respecto de cómo resolvieron, (o cómo van resolviendo); donde discutan diversidad de procedimientos, de representaciones, de resultados; donde existan variadas oportunidades de enfrentarse a la toma de decisiones en problemas de diferentes características: de solución única y de varias soluciones, expresados en forma coloquial o a través de símbolos y números; vinculados a algún contexto extramatemático o intramatemático, con datos innecesarios y otros donde parezca que estos datos faltan o haya que buscarlos…

La labor de cada docente, tarea para nada sencilla, es pensar cómo organizar y gestionar instancias de discusión en el aula a partir de esos “cómo”. Sostenemos que los problemas son los disparadores para estos momentos que:

(…) conforman una de las modalidades que adquiere la interacción entre pares en el aula (…) De ninguna manera constituyen “eventos naturales” de la vida en el aula. Las discusiones no pueden quedar libradas a las contingencias de una clase o a la  espontaneidad de los alumnos… deben ser organizadas intencional y sistemáticamente por el maestro a quien corresponde un papel central e insustituible en su desarrollo (Quaranta-Wolman, 2003, p. 189).

Si pensamos la gestión de la clase con estos momentos de discusión, la inclusión de la multiplicación podría tener lugar desde primer grado con algunas situaciones que impliquen las “sumas de iguales” de dos o más sumandos para, en segundo grado incorporar la simbología incluyendo problemas del campo multiplicativo a la vez que se profundizan los del campo aditivo. También sabemos, tal como afirman Itzcovich, et. al. en La Matemática Escolar, (2008, p. 89) que se requiere de todo el trayecto de la escolaridad primaria “(…) para que los alumnos puedan identificar los diferentes problemas que estas herramientas permiten resolver, logren dominar la variedad de relaciones numéricas que es posible establecer y elaboren los diversos recursos de cálculo que es pertinente disponer”.  

¿Cómo comenzamos? 

Situaciones como: ¿Cuántas masitas hay en 8 bolsitas si cada una trae 6 masitas? ¿Cuántas figuritas tendremos en 7 paquetes si cada uno trae 4 figuritas? ¿Cuántas ruedas se necesitarán para armar 5 bicicletas?, ¿cuántas para 4 triciclos?, son propuestas que podrán ser abordadas desde primero y segundo grado. 

A partir de situaciones de este tipo, que se desprendan de un contexto que sea interesante y que atrape, las niñas y los niños irán organizando y construyendo sus conocimientos en relación al campo operatorio. Pero no alcanza con resolver problemas, se requiere un trabajo de reflexión, discusión, argumentación y validación de las respuestas, acuerdos e institucionalizaciones en torno a las situaciones de modo que el trabajo esté cargado de significados y construcciones personales y colectivas. Del mismo modo, la inclusión de la simbología convencional y de los algoritmos también requiere de tiempo y de un trabajo sistemático de construcción ya que “el dominio de un procedimiento particular, el reconocimiento de su eficacia en tal tipo de resolución se construye en un tiempo largo, alternando fases de resolución de problemas y fases de ejercitación sistemática, en particular para los procedimientos reconocidos como importantes” (Sáiz, I. y Parra, C., 1992, p. 23)

Para profundizar con el análisis de algunos problemas y sentidos es importante que caractericemos a la operación y lleguemos a algunos acuerdos. 

Multiplicar significa, en su nivel más intuitivo, reiterar una cantidad; sin embargo, los dos elementos de una multiplicación responden a contextos totalmente diferentes: uno de ellos, la cantidad que se repite (el multiplicando) es un número cardinal concreto, mientras que el otro factor (el multiplicador) que indica las veces que se repite la cantidad inicial, es una suerte de cardinal de cardinales (Cortés, 2002, p. 23). 

El símbolo de esta operación se representa con “x” o con “.”. Desde la didáctica de la Matemática decimos que la Multiplicación va más allá de la simple suma reiterada o de la conceptualización de “suma abreviada”. Avancemos con algunos problemas tipo del  campo multiplicativo:

1. Ranaldo tiene el quíntuple de piedras que su primo Pederiko. Pederiko tiene 3 piedras, ¿Cuántas tiene Ranaldo?
2. Ranaldo embocó 5 de sus piedras dentro del triángulo, donde cada piedra vale tres puntos. ¿Cuántos puntos obtuvo?

Ambas situaciones se resuelven mediante una multiplicación “por 5”, sin embargo podemos pensarlas como dos tipos de relaciones diferentes: la primera implica una relación de un solo espacio de medida ya que involucra una sola “clase de elementos”: “piedras”. El resultado del quíntuple de piedras es 15 piedras.

La segunda situación, involucra dos espacios de medidas; es decir, dos clases de elementos: “piedras” y “puntos”:

1 piedra     –   3 puntos

 5 piedras   –   15 puntos

Vergnaud organiza las situaciones multiplicativas en tres categorías (Fajardo, M., Gálvez, G. 2019, p. 8):

Un solo espacio de medidas: Las denomina “Único espacio de medidas” ya que aparece un solo tipo de elementos relacionados con un operador escalar.

Dos espacios de medidas: “Isomorfismo de Medidas”, ya que a cada elemento de una clase le corresponde una cantidad determinada de elementos de la otra clase. Son llamadas también de Proporcionalidad directa.

Tres espacios de medidas: “Producto de Medidas”. Son aquellas en las que intervienen tres espacios. También llamados problemas de Conteo o Combinatorias. Su estructura consiste en la composición de dos espacios de medidas, lo que genera un tercer espacio. 

1. Ranaldo se quiere vestir antes de ir a jugar. Tiene tres pantalones: liso, rayado y estampado. Tiene 5 remeras de distintos colores: amarilla, roja, azul, violeta, marrón. ¿De cuántas maneras distintas podrá vestirse para el juego?

Observen que también esta situación se resuelve con 3 x 5 como la 1) y la 2), pero aquí se tienen tres espacios de medida:  pantalones – remeras – combinaciones (pantalón liso – remera amarilla, pantalón  liso – remera roja, pantalón liso – remera azul, pantalón liso – remera violeta, …)

En estas categorías que propone Vergnaud sobre las situaciones multiplicativas no queremos dejar de destacar a los “Sentidos o significados de la Multiplicación”. Así como las operaciones de Adición y Sustracción que abordamos en anteriores Acciones Formativas, se pueden categorizar según distintos significados, proponemos lo mismo para la Multiplicación. Además de los ya enunciados Proporcionalidad y Combinatoria podemos agregar el de Organizaciones rectangulares. Este sentido de la multiplicación aborda situaciones en las que se relacionan filas y columnas, en las que hay que contar cantidad de baldosas u objetos ordenados en una distribución rectangular. Algunas propuestas podrán ser:

En estas dos distribuciones tenemos la misma cantidad de piedras ¿En cuál te parece más rápido contarlas? ¿Cómo harías para contarlas? ¿Hay alguna forma más rápida?

Sugerimos que la diversidad de situaciones que se presenten en el aula sean propicias para la discusión sobre los distintos sentidos de la multiplicación y no quedarse en el concepto limitado de la multiplicación como suma reiterada. Uno de los propósitos esenciales de la enseñanza de la matemática es precisamente que lo que se ha enseñado esté cargado de significado, tenga sentido. En particular, para la multiplicación será valioso que se reconozca qué tipo de problemas resuelve, que situaciones no pueden ser resueltas por dicha operación, qué propiedades la caracterizan, con qué otros conceptos y operaciones se relaciona. 

 

4- RESOLVEMOS, CREAMOS Y PROPONEMOS

 

Observamos junto a niñas y niños el video de Ranaldo jugando junto a su primo.

 

https://www.youtube.com/watch?v=a5zxgJyV2hM

 

Abrimos el diálogo:

¿A qué están jugando Ranaldo y Pederiko?

¿Qué diferencias y similitudes encuentran con los juegos que nos venía proponiendo Ranaldo?

¿Cómo piensan que se obtiene mayor cantidad de puntos?

¿Cómo se cuentan los puntos de las piedras que cayeron fuera?

¿Cómo se cuentan los puntos de las piedras que cayeron dentro?

 

Ambientamos el aula o el patio. Las y los invitamos a organizarse en grupos de 4 o 6 integrantes dependiendo las características del grado (en otra instancia serán 2 contra 2 o 3 contra 3). Se deberá trazar el triángulo para jugar. Será interesante la discusión sobre la construcción, la distancia desde dónde tirar, las dimensiones del triángulo, pero sugerimos que la misma se haga previamente o en instancias posteriores. En lugar de piedras, utilizaremos otro material que las represente; pueden ser botones o bollitos de papel. Les preguntamos a ellas y a ellos con qué otro elemento se podría reemplazar. Podemos comenzar con 6 “piedras” e ir variando la cantidad. Aquí solo invitaremos a contabilizar los puntos de uno de los participantes o grupo de participantes. La comparación entre los puntos para definir quién obtuvo más requiere de saberes previos ya abordados en las Acciones Formativas anteriores. 

 

Repreguntamos:

 ¿Cómo contamos los puntos de las piedras que caen fuera? 

¿Y de las que caen dentro? 

Simulamos un juego tirando 6 “piedras” todas del mismo color (que corresponde a un mismo participante o grupo en lugar de las cuatro piedras como se propone en el video). 

Les solicitamos que piensen y que, en primera instancia, calculen de manera individual y, posteriormente, en los grupos de trabajo: ¿Cuántos puntos obtiene un jugador (o su grupo) si las fichas quedan de esta manera? (A modo de ejemplo compartimos una posible jugada para su análisis. Será mucho más enriquecedor si la propuesta sobre la que se discute es aquella que surge en el aula).

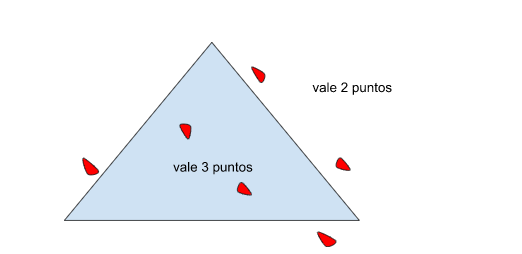
Es importante:

– generar en el aula un clima de trabajo propicio para que surjan diversas estrategias de resolución, personales y grupales, teniendo confianza en las propias posibilidades;

– analizar algunas de las posibles resoluciones que puede tener una misma situación;

– organizar la clase para que las niñas y los niños expliciten las resoluciones y argumenten sobre su validez, seleccionando algunas de las producciones para discutir, de manera que haya variadas opciones para entrar en diálogo;

– generar espacios de discusión sobre las ventajas y desventajas de una u otra resolución;

– analizar errores e hipotetizar sobre por qué pudieron haber ocurrido.

 

Entre las posibles resoluciones y registros que las niñas y los niños pueden realizar, podríamos encontrar:

 

a. Registro figural-icónico de la jugada, acompañado por registros numéricos y de la lengua natural para el conteo de los puntos. 

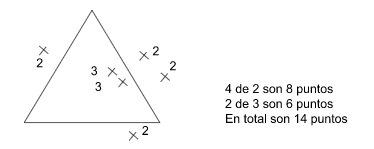
b. Registro figural-icónico y de la lengua natural incorporando registro numérico (expresiones simbólicas: números y operaciones).

c. Registro figural-icónico y registro de la lengua natural. En este caso se omite dar el resultado final, sólo se obtienen los puntos parciales.

d. Registro tabular: Organización de datos en tablas. Esta resolución responde a una representación que da cuenta de cierto reconocimiento de las series proporcionales: cantidad de piedras y puntos obtenidos por cada una.

e. En algunas ocasiones las niñas y los niños podrán optar por contar las piedras de dos en dos y de tres en tres respectivamente. Esta es una acción poco frecuente al inicio pero que se refiere a la construcción de las escalas y es un atrayente lugar para abrir la discusión.

 

A partir de las resoluciones que pudieran surgir en el aula, será interesante debatir en torno a las distintas formas de resolver, a la necesidad  de recurrir a algún tipo de registro: gráficos-icónicos, tabulares, numéricos, de la lengua natural para tomar decisiones sobre aquel más económico o más pertinente para comunicar aquello que se desea expresar.

 

Algunos acuerdos o institucionalizaciones:

• Para contar más fácilmente los puntos de las piedras puedo reiterar los puntos que vale cada una según la cantidad de piedras mediante una adición.
• Para contar más fácilmente los puntos de las piedras que caen fuera puedo ir contando de dos en dos.
• Para contar más fácilmente los puntos de las piedras que caen dentro puedo ir contando de tres en tres. 

 

¡A jugar!

En este momento, se puede proponer jugar para realizar el cálculo de los puntos de cada grupo y el análisis comparativo de los mismos para intensificar lo abordado sobre sustracción en la Acción Formativa N° 95.

Nos metemos en el mundo matemático

1- Pederiko y Ranaldo volvieron a jugar (Ranaldo tiene piedras rojas y Pederiko amarillas) ¿Quién ganó esta vez?  

¿Cómo te das cuenta quién obtuvo más puntos?

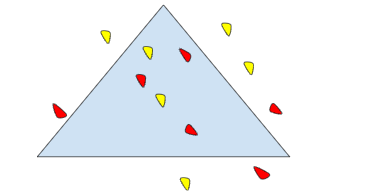
2- Si para saber cuántos puntos obtuvo se registró lo siguiente:

2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 =

3 + 3 + 3 + 3 =

¿Cómo sería el tablero?

 

3- ¿Te animás a inventar un tablero en el que se pueda obtener estos puntos?

2 + 2 + 2 + 2 =

3 + 3 + 3 + 3 + 3 + 3 =

4 + 4 =

 

4- Podrías ayudar a los chicos a saber cuántos puntos obtuvieron si registraron lo siguiente:

 

2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 =

3 + 3 + 3 + 3 + 3 =

4 + 4 + 4 + 4 + 4 + 4 =

 

5- A un grupo se le mojó el papel donde habían registrado los puntos ¿Los ayudás a completar lo que se les borró?

 

4 + 4 + 4 + ………………………………………….. + 4 = 36

2 + 2 + 2 + ………………………………………………….. = 20

5 + 5 + ……………………………….. + 5  = 25

 

¿Cómo te imaginás un tablero que incluya el último registro?

¿Qué te llama la atención de estos tipos de adiciones que realizamos cuando contamos los puntos? 

¿Podremos encontrar una forma más corta de escribir estos cálculos? 

 

Podríamos tensionar la necesidad de economizar los pasos para incorporar el símbolo de la multiplicación a partir de la cantidad de repeticiones. ¿Cuántas veces cuento “dos puntos”? ¿Cuántas veces cuento “tres puntos”?

Aquí se podrían retomar algunos dichos de los chicos:

 

el 2 sumado 4 veces – 4 de 2 son 8   –   4 veces 2 son 8    –     2 repetido 4 veces        

el 3 sumado 6 veces – 2 de 3 son 6   –   2 veces 3 son 6    –     3 repetido 2 veces

 

¿Cuál es el sumando que se reitera? ¿Cuántas veces? 

 

Concluimos:

Cuando contamos los puntos de las piedras que caen fuera, el sumando que se repite es el dos. La cantidad de veces que se repite es 4. 

 

Es una buena oportunidad para incorporar el símbolo de la multiplicación, signo “x” y formalizar el concepto de esta operación que se viene trabajando en la presente Acción Formativa.

 

Podremos escribirlo de distintas maneras para concluir con el registro de una forma más económica:

 

Adición de piedras que valen 2	Lenguaje coloquial	Multiplicación	Resultado
2 + 2	2 repetido dos veces	2 x 2	4
2 + 2 + 2	2 repetido tres veces	2 x 3	6
2 + 2 + 2 + 2	2 repetido 4 veces	2 x 4
2 + 2 + 2 + 2 + 2	2 repetido 5 veces	2 x 5
2 + 2 + 2 + 2  + 2 + 2		2 x 6
2 + 2 + 2 + 2  + 2 + 2 + 2		2 x 7
			16
	2 repetido 9 veces
		2 x 10
		2 x 11
			24

 

Invitamos a completar la grilla.

 

Una posible acción para dar continuidad a la presente secuencia es la presentación de otros problemas que impliquen multiplicaciones por dos y por tres para poner en discusión que los cálculos ya resueltos "sirven" para otras situaciones y dar sentido a la grilla que se presentó como recurso al cual recurrir. De esta manera, se podrá proseguir en próximas clases en las que se planifique la incorporación de repertorios de cálculos, cálculos memorizados, productos básicos o tablas, e incursionar en la construcción y uso de la tabla pitagórica.

 5- BIBLIOGRAFÍA

• Charnay, R. (1994). “Aprender por medio de la resolución de problemas”. En Parra, C. Sainz, I. (Comps.). “Didáctica de Matemáticas. Aportes y reflexiones” . Buenos Aires: Paidós Educador.
• Fajardo, M., Gálvez, G., Pino, K., Ramírez, A. (2017-2019) Situaciones Multiplicativas. [Archivo PDF]. Recuperado de https://cmmedu.uchile.cl/wp-content/uploads/2020/02/Situaciones-multiplicativas.pdf
• Itzcovich, H., Ressia de Moreno, B., Novembre, A., Becerril, M., Gvirtz, S. (2008). “La matemática escolar: Las prácticas de enseñanza en el aula”. Buenos Aires: Aique Grupo Editor.
• Castro, A., Díaz, A., Escobar, M:, Fernández, A., Penas, F., Ponce, H.,  . . . Wolman, S. (2009). “Enseñar matemática en la escuela primaria”. Buenos Aires: Tinta Fresca.
• Cortés, G. (2002). “Para contar y contar. Apuntes metodológicos. Cómo enseñar para aprender Matemática”. Buenos Aires: Stella.
• Ministerio de Educación, Ciencia y Tecnología de la Nación (2004). Núcleos de Aprendizajes Prioritarios. 1º Ciclo EGB – Nivel Primario. Matemática. Buenos Aires, Argentina. 
• Ministerio de Educación, Ciencia y Tecnología de la Nación (2004). Serie cuadernos para el aula: Matemática 2. Buenos Aires, Argentina.
• Parra, C., Sáiz, I. (2007) “Enseñar aritmética a los más chicos: de la exploración al dominio”. Rosario: Homo Sapiens.
• Quaranta, M., Wolman, S. (2003) “Discusiones en la clase de matemática: Qué, para qué y cómo se discute” en Panizza, M. (comps.) “Enseñar matemática en el Nivel Inicial y en el primer ciclo de EGB”. Buenos Aires: Paidós.

 

Agradecemos a Mariela Pagani, Carla Alario, Romina Sequier y Alejandro Alessi que redactaron la presente Acción Formativa y forman parte del Equipo Pedagógico de la Subsecretaría de Educación Primaria. Agradecemos la colaboración de Gustavo Chinellato en la producción del material audiovisual.

 

¡Nos seguimos encontrando en este espacio!

 

Subsecretaría de Educación Primaria.